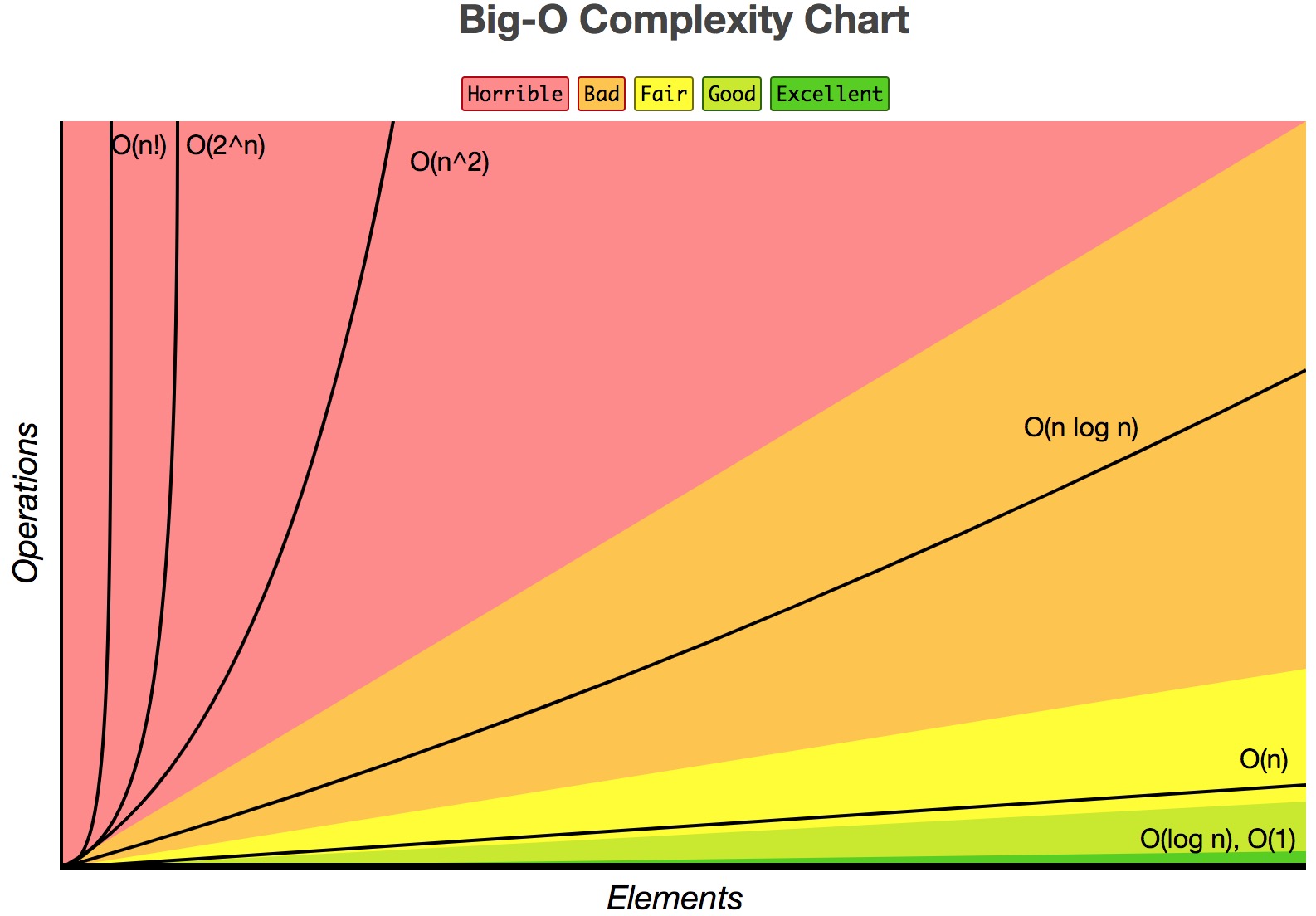
Типичные Big O классификации с примерами

O(1) – Постоянное время

 Самая эффективная сложность, где время выполнения остается постоянным независимо от размера входных данных.

PHP Пример: Доступ к элементу массива по индексу.

$array = [1, 2, 3, 4, 5];
echo $array[3]; // Доступ к элементу массива - операция O(1)

SQL Пример: Чтение строки данных по первичному ключу.

SELECT * FROM users WHERE id = 5; -- Поиск по первичному ключу - операция O(1)

O(log n) – Логарифмическое время

Эффективность выше, чем у линейного времени, так как время выполнения увеличивается логарифмически с увеличением размера входных данных.

PHP Пример: Бинарный поиск в отсортированном массиве.

function binarySearch($arr, $x) {
    $left = 0; 
    $right = count($arr) - 1; 
    while ($left <= $right) { 
        $mid = floor(($left + $right) / 2); 
        if($arr[$mid] == $x) return true; 
        else if ($arr[$mid] < $x) $left = $mid + 1; 
        else $right = $mid - 1; 
    } 
    return false; 
}

SQL Пример: Поиск с индексированием в большой таблице.

SELECT * FROM users WHERE age = 30; -- Использование индекса улучшает поиск до O(log n)

O(n) – Линейное время

Время выполнения увеличивается линейно в зависимости от размера входных данных.

PHP Пример: Перебор всех элементов массива.

$array = [1, 2, 3, 4, 5];
foreach ($array as $element) {
    echo $element;
}

SQL Пример: Поиск по неиндексированному столбцу.

SELECT * FROM users WHERE name = 'John'; -- Линейный поиск, если столбец name не индексирован

O(n log n) – Линейно-логарифмическое время

Более сложно, чем линейное время, но обычно эффективнее, чем квадратичное время. Часто встречается в эффективных алгоритмах сортировки.

PHP Пример: Сортировка массива с помощью алгоритма сортировки слиянием.

sort($array); // Большинство встроенных функций сортировки работают за O(n log n)

// или QuickSort - классический алгоритм сортировки с временной сложностью в среднем O(n log n). 
// Он выбирает опорный элемент из массива и разделяет остальные элементы на две группы, 
// больше и меньше опорного. Затем он рекурсивно сортирует эти подгруппы.
function quickSort($array) {
    if (count($array) < 2) {
        return $array;
    }

    $left = $right = array();
    reset($array);
    $pivot_key = key($array);
    $pivot = array_shift($array);

    foreach ($array as $k => $v) {
        if ($v < $pivot)
            $left[$k] = $v;
        else
            $right[$k] = $v;
    }

    return array_merge(quickSort($left), array($pivot_key => $pivot), quickSort($right));
}

$array = [5, 3, 2, 4, 1];
$array = quickSort($array);
print_r($array);

В этом примере функция quickSort реализует алгоритм быстрой сортировки. Она выбирает первый элемент массива в качестве опорного и разделяет оставшиеся элементы на две группы. Затем рекурсивно применяет себя к этим группам, пока массив не будет полностью отсортирован. Этот метод эффективен и демонстрирует O(n log n) производительность на большинстве наборов данных.

SQL Пример: Создание индекса в таблице.

CREATE INDEX idx_name ON users(name); -- Создание индекса требует O(n log n) времени

O(n²) – Квадратичное время

Время выполнения увеличивается квадратично по отношению к размеру входных данных. Это обычно менее эффективно, особенно для больших наборов данных.

PHP Пример: Вложенные циклы для обработки элементов массива.

for ($i = 0; $i < count($array); $i++) {
    for ($j = 0; $j < count($array); $j++) {
        // Выполняется O(n²) раз
    }
}

SQL Пример: Сложные запросы со множественными JOIN, особенно без индексов.

SELECT * 
FROM users u 
JOIN orders o ON u.id = o.user_id; -- Может быть O(n²), если нет индексов

O(2^n) и O(n!) – Экспоненциальное и факториальное время

Самые неэффективные классификации, где время выполнения растет экспоненциально или факториально. Эти сложности обычно непрактичны для больших наборов данных из-за их чрезвычайно высокого времени выполнения.

O(2^n) – Экспоненциальное время

Часто встречается в рекурсивных алгоритмах, где каждый вызов функции порождает два или более вызовов.

Пример: Рекурсивное вычисление чисел Фибоначчи

function fibonacci($n) {
    if ($n <= 1) {
        return $n;
    }
    return fibonacci($n - 1) + fibonacci($n - 2);
}

echo fibonacci(10); // Вызов этой функции приведет к экспоненциальному количеству вызовов функции

Этот алгоритм имеет экспоненциальную временную сложность, так как каждый вызов fibonacci порождает два дополнительных вызова.

O(n!) – Факториальное время

Встречается в алгоритмах, которые включают перебор всех возможных комбинаций.

Пример: Генерация всех перестановок массива

function generatePermutations($array, $size, $n) {
    if ($size == 1) {
        print_r($array);
    }

    for ($i = 0; $i < $size; $i++) {
        generatePermutations($array, $size - 1, $n);

        if ($size % 2 == 1) {
            $temp = $array[0];
            $array[0] = $array[$size - 1];
            $array[$size - 1] = $temp;
        } else {
            $temp = $array[$i];
            $array[$i] = $array[$size - 1];
            $array[$size - 1] = $temp;
        }
    }
}

$array = [1, 2, 3];
generatePermutations($array, count($array), count($array));

Этот алгоритм генерирует все возможные перестановки массива. Количество перестановок для массива из n элементов равно n!, что делает временную сложность этого алгоритма факториальной.